
|
研究领域
长期致力于计算力学与智能计算方法研究,聚焦柔性结构计算力学、多场耦合系统仿真和国产CAE软件研发三大方向。针对航天航空、特殊装备等国家重大需求中的关键力学问题,开展原创性理论方法研究和技术创新,形成了特色鲜明的研究体系。研究成果在柔性结构褶皱分析、密闭空间气氛演化建模、自主可控CAE求解器开发等方面取得进展,相关技术已成功应用于多个重要工程领域,为提升我国装备数字化的仿真能力提供了坚实的技术支撑。
1.柔性结构计算力学
1.1 柔性薄膜结构
柔性薄膜在航天工程中具有重要应用价值,包括太阳帆(图1)、太阳翼和反射天线等关键部件。充气薄膜结构凭借其轻质、可折叠、易展开等优异特性,在航天领域备受青睐,已成功应用于太阳帆充气桅杆、柔性充气太空舱等先进航天器。

图1.可展开柔性薄膜太阳帆
针对薄膜褶皱现象,基于张力场理论,创新性地建立了薄膜结构褶皱变形的无压缩材料模型;从变分原理源头出发,系统推导并证明了无压缩、无拉伸材料非线性分析的统一参变量势能原理和余能原理,提出了能够精确模拟薄膜褶皱演化过程的互补有限元方法。通过对屈服函数进行线性化处理,将原非线性问题转化为系列线性互补方程求解,有效避免了常规牛顿类迭代方法在分析无拉伸(无压缩)材料时的收敛困难。已成功应用于薄膜结构的无褶优化设计,显著提高了设计效率(图2)。
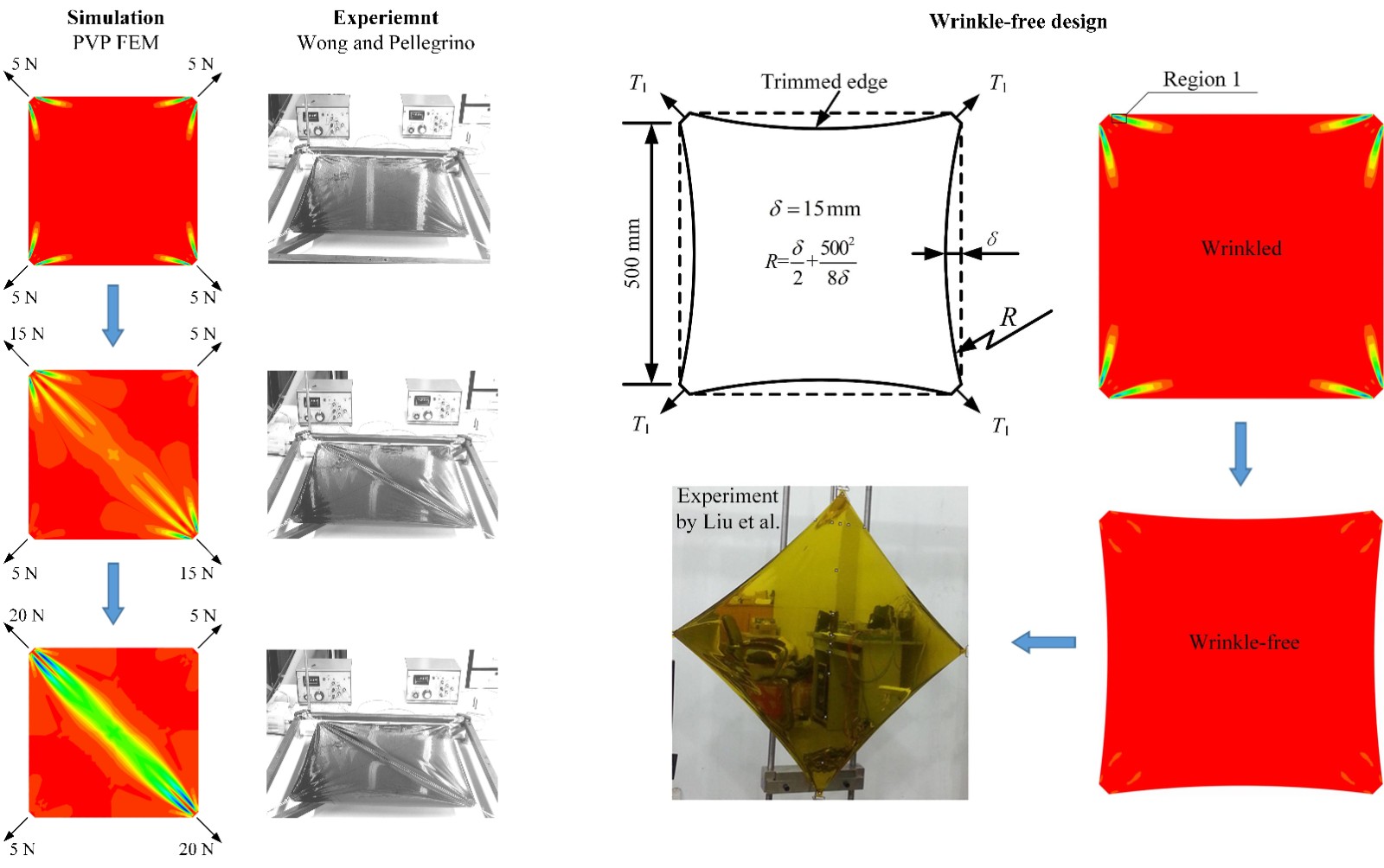
图2.方膜对角拉伸数值模拟与无褶设计
该方法进一步结合共旋有限元方法,开发的PVP-CR方法已成功应用于方形气囊等典型充气结构的承载大变形分析,数值模拟结果与实验测试高度吻合(图3)。
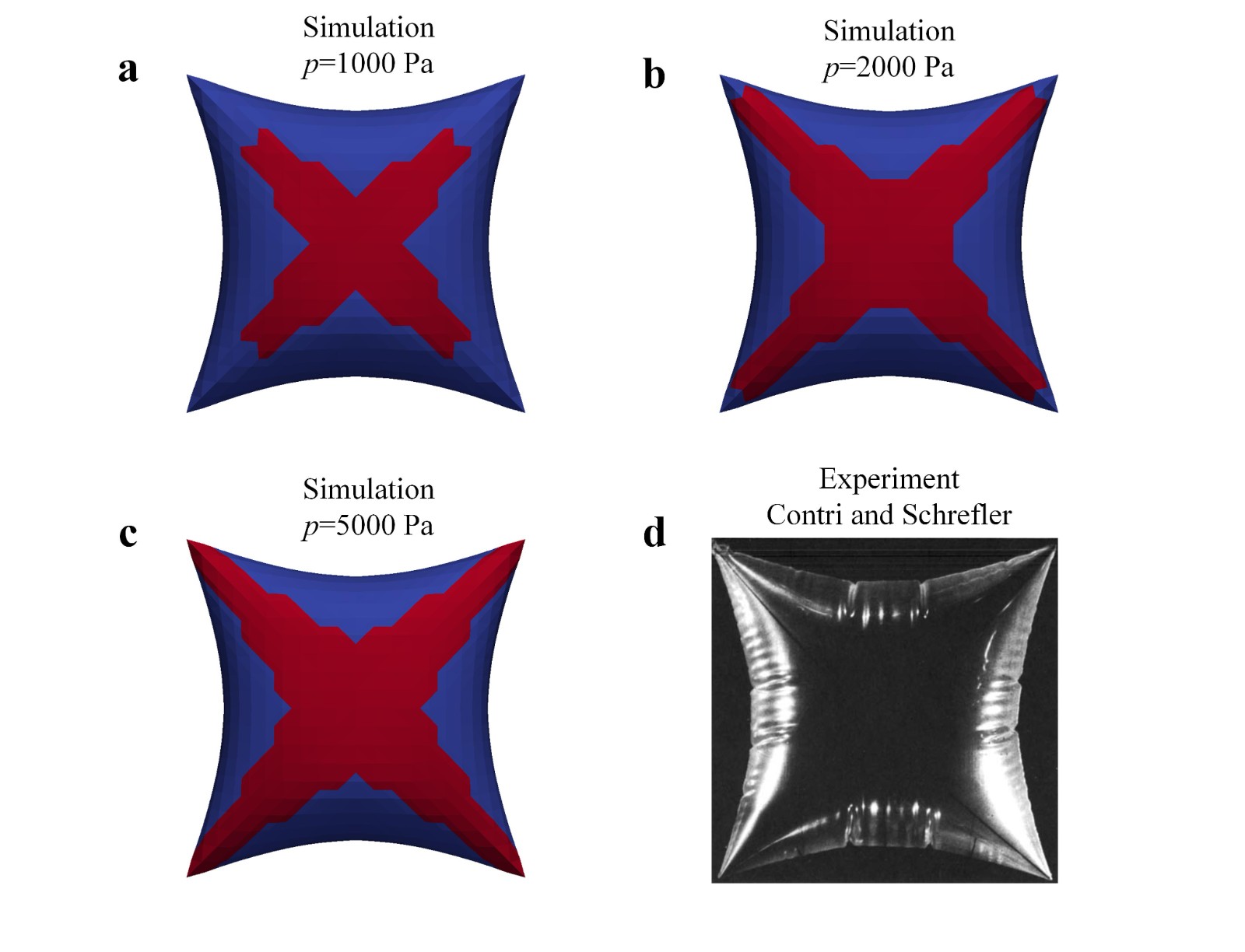
图3.方形气囊充气大变形模拟与实验验证
1.2 柔性索网结构
可展开结构广泛应用于太阳能电池板、索网天线等的支撑结构(图4)。传统可展结构存在着复杂的刚性节点和伸缩杆展开等缺陷,解决这些问题的一个可能的方案是基于张拉整体的概念来设计可展开结构。其独特的结构形式也带来了独特的性质,例如强度重量比高、柔性可控、抗冲击性能强等性质。这些性质使其在诸多领域具有应用潜力。

图4.柔性太阳翼张拉整体支撑结构与模块化索网天线
采用参变量共旋算法解决张拉整体结构数值模拟的收敛性问题,将结构大变形分解为结构整体坐标下的刚体位移和单元局部坐标下的小应变变形。算法表现出良好的稳定性,并能准确预测张拉整体结构中松弛绳索的分布情况,可为结构工程师提供可靠的数值参考和指导。该方法被成功地应用到上海航天八院某铰接式伸展机构等张拉整体支撑结构的行为预测和结构找型(图5),数值模拟分析结果受到好评。
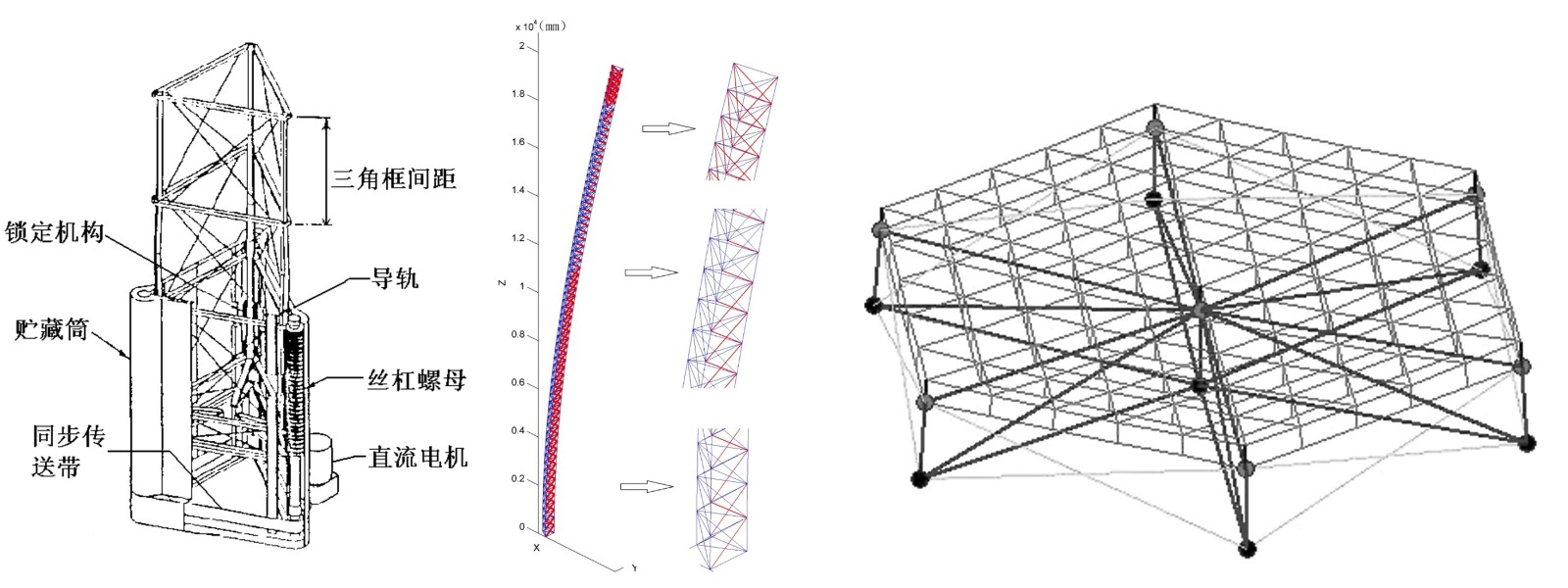
图5.张拉整体支撑结构变形预测与索网天线单胞找形结果
1.3 基于数据驱动的张拉整体机器人步态设计
基于张拉整体概念的软机器人和柔性臂结构因其轻量化、低成本和卓越的环境适应性而成为研究热点。创新性地提出了杆件屈曲驱动方式,这一方法显著减少了作动器数量并大幅提升了整体系统的抗冲击性能。
采用数据驱动的“混合孪生”方法,增强了贪婪搜索算法生成步态规划的能力。通过制作两种不同驱动方式的张拉整体机器人原型(杆件屈曲驱动与绳索收缩驱动),并利用运动捕捉系统和高速摄像机进行行走和冲击试验(图6、图7),验证了杆件屈曲驱动结构在自重和抗冲击性方面的显著优势。杆件屈曲驱动的概念可以在基于张拉整体结构的连续臂中找到更多的应用,特别是在需要减振或隔离功能的领域。
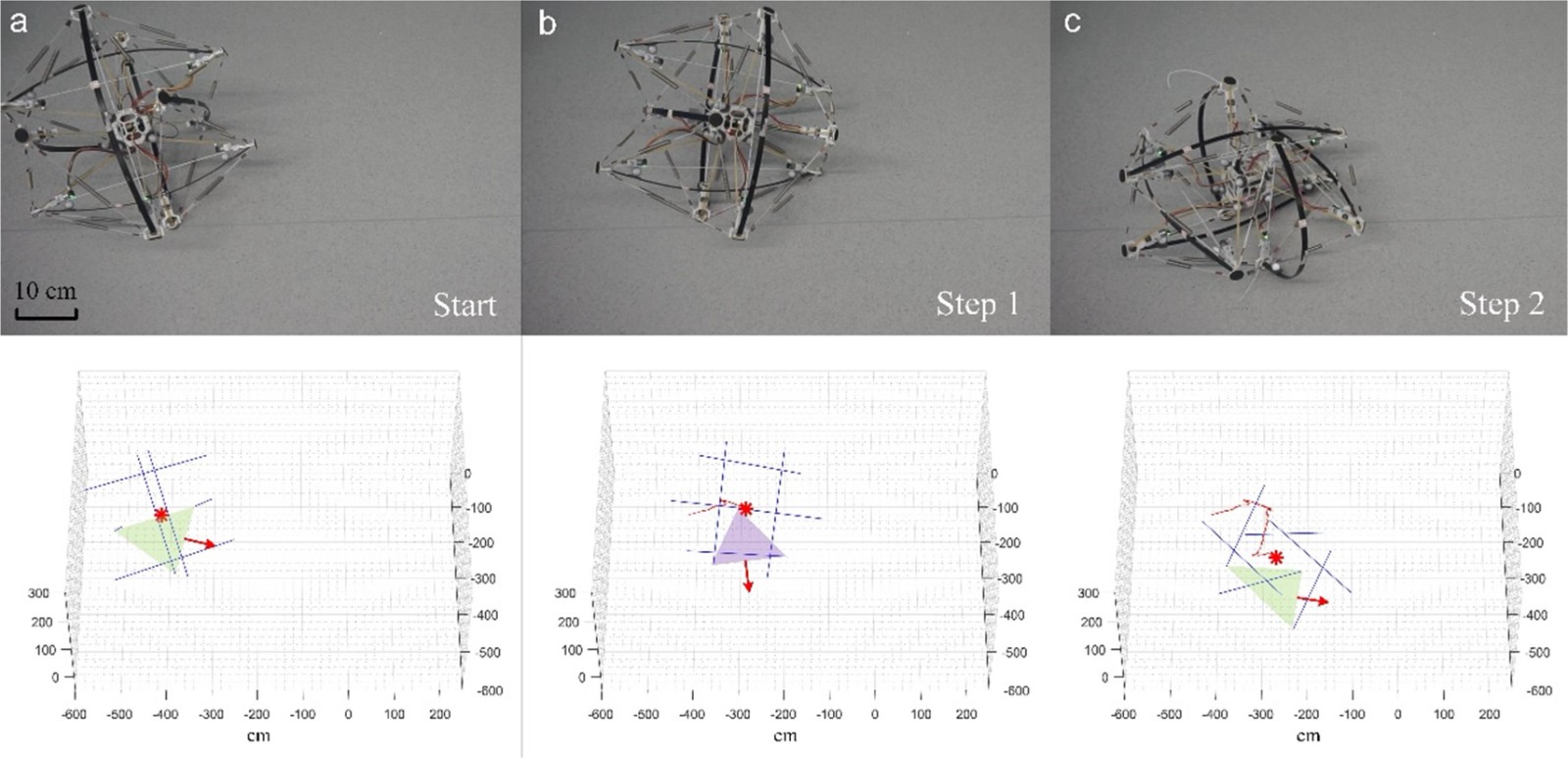
图6.张拉整体机器人行走瞬时摄影
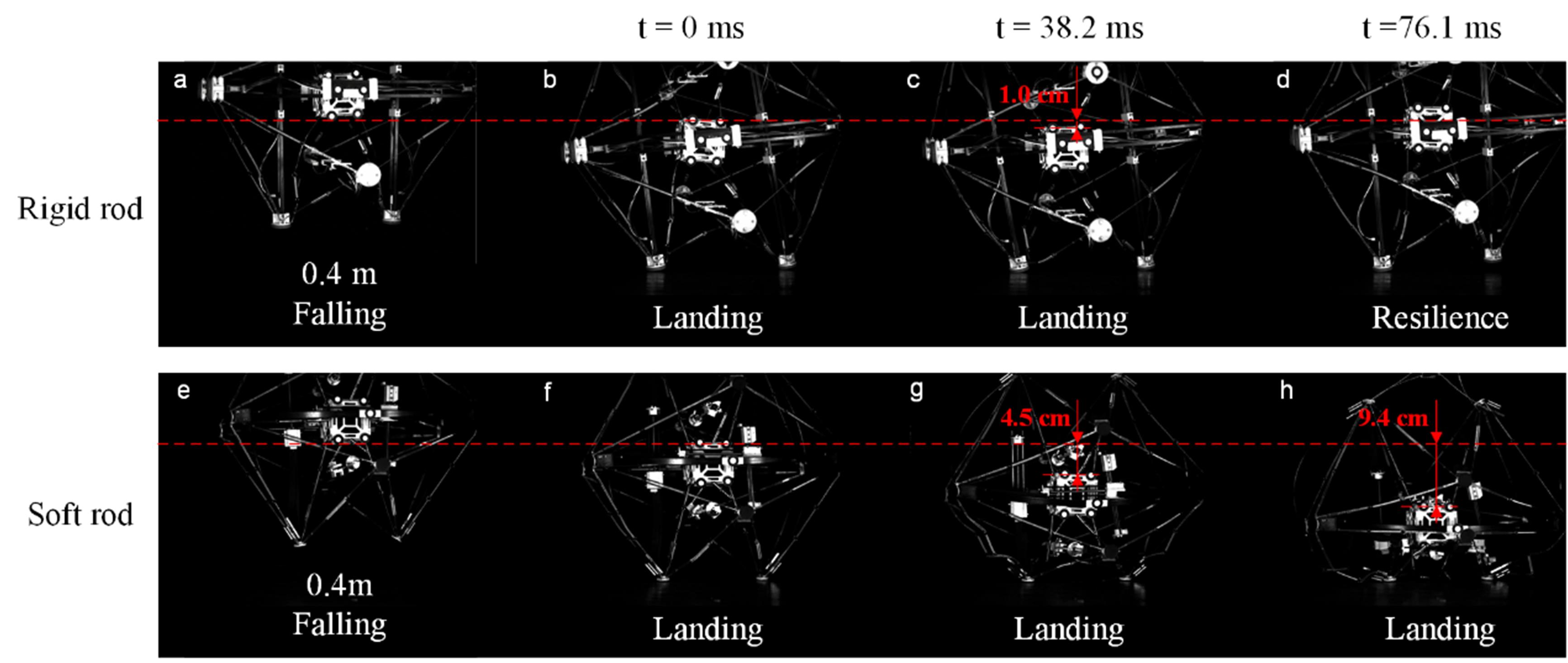
图7.张拉整体机器人跌落实验瞬时摄影
创新之处:
① 建立了薄膜褶皱分析的互补有限元方法,计算效率比常规方法提10-20倍;
② 索网天线结构力学分析方法比著名的BFGS算法效率提高约5-10倍;
③ 开发了参变量共旋有限元方法,解决了商业软件的收敛困难问题;
④ 提出了杆件屈曲驱动创新方法,显著提升系统抗冲击性能。
代表论文:
[1] Mengkai Lu, Liang Zhang*, Xingjie Chen, Anatoly Vershinin, Variational formulations of no-tension/compression solids and the applications to masonry and wrinkled membrane, International Journal of Solids and Structures, 2023, 275: 112298. https://doi.org/10.1016/j.ijsolstr.2023.112298
[2] Zhang L*, Dong KJ, Lu MK, Zhang HW, A wrinkling model for pneumatic membranes and the complementarity computational framework, Computational Mechanics, 2020, 65(1): 119-134. https://doi.org/10.1007/s00466-019-01755-7
[3] Zhang L, Gao Q, Zhang HW*, Analysis of 2-D bimodular materials and wrinkled membranes based on the parametric variational principle and co-rotational approach, International Journal for Numerical Methods in Engineering, 2014, 98(10): 721-746. https://onlinelibrary.wiley.com/doi/10.1002/nme.4649

